28 Lutego 2024 o godz. 12:00, odbyła się obrona pracy doktorskiej mgra inż. Przemysława Sebastjana, pt.: „Optimization of automotive suspension components with consideration of their unstable behavior”.
Promotorem rozprawy był dr hab. inż. Wacław Kuś prof. PŚ, natomiast recenzentami dr hab. inż. Marta Kurek prof PO z Politechniki Opolskiej, dr hab. inż. Monika Pernach prof. AGH z Akademii Górniczo-Hutniczej w Krakowie oraz prof. dr hab. inż. Wojciech Sumelka z Politechniki Poznańskiej. Komisja Doktorska uchwaliła wnioski do Rady Dyscypliny Inżynieria Mechaniczna o nadanie mgr inż. Przemysławowi Sebastjanowi stopnia doktora nauk technicznych w dyscyplinie Inżynieria Mechaniczna oraz o wyróżnienie pracy doktorskiej.
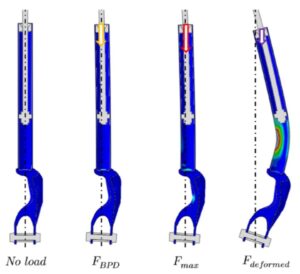
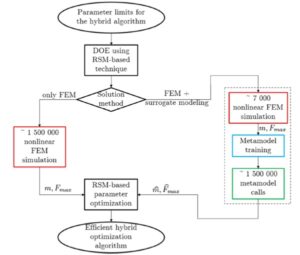
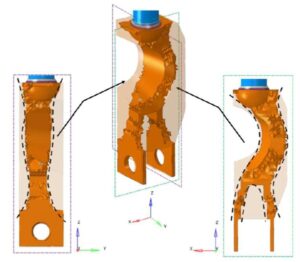
Rozprawa „Optimization of automotive suspension components with consideration of their unstable behavior” dotyczy zagadnienia optymalizacji kształtu komponentów amortyzatora samochodowego pod kątem masy, jednak z uwzględnieniem ograniczeń związanych ze statecznością całego układu zawieszenia. W pierwszej części dysertacji przedstawiono niezbędne podstawy teoretyczne do zrozumienia i odtworzenia procesu optymalizacji, włączając w to zasadę działania oraz rolę amortyzatorów samochodowych, symulowanie ich pracy pod działaniem krytycznych obciążeń z wykorzystaniem metody elementów skończonych, oraz techniki optymalizacji i metamodelowania. W części głównej skupiono się na adaptacji i rozszerzeniu istniejących metod modyfikacji topologii i kształtu części do rozpatrywanego zagadnienia, proponując dwie metody oparte o niejawny opis geometrii: przestrzenną metodę poziomic oraz metodę rzutowania. Parametry zmienne z obu metod połączono z zaproponowanym hybrydowym algorytmem optymalizacji, składającym się z kolejno wykonywanych: algorytmu genetycznego (w jednej z dwóch odmian) oraz strategii ewolucyjnej (1 + 𝜆). Następnie ów hybrydowy algorytm optymalizacji poddano procesowi dostosowania operatorów genetycznych oraz parametrów funkcji kary w celu zwiększenia jego efektywności przy założonych więzach co do całkowitej ilości wykonanych iteracji (symulacji). W tym celu najpierw stworzono dwie grupy metamodeli spośród których wybrano najlepiej rokujące: sztuczną sieć neuronową oraz Kriging. Posłużyły one do zastąpienia kosztownej analizy MES przy ich wielokrotnym użyciu, w celu wykonania założonego eksperymentu opartego o metodę powierzchni odpowiedzi, co umożliwiło weryfikację nieliniowości oddziaływania parametrów wejściowych algorytmu hybrydowego (operatory genetyczne, parametry funkcji kary) na jego zdolność do minimalizacji masy układu zawieszenia przy zachowaniu jego stateczności. Tak dostosowany algorytm zweryfikowano w końcowej części pracy na dwóch rzeczywistych przykładach przemysłowych: optymalizacji pasywnego oraz półaktywnego amortyzatora samochodowego. Porównano obie metody modyfikacji geometrii oraz dwie wersje algorytmu hybrydowego, jak również możliwości metamodelowania do zastąpienia rzeczywistego modelu opartego o symulacje MES. Całość pracy wieńczy podsumowanie, dyskusja wyników oraz sformułowanie dalszego zakresu pracy nad zagadnieniem optymalizacji amortyzatorów samochodowych pod kątem ich masy z uwzględnieniem stateczności całego układu zawieszenia.