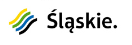The boundary element method (BEM) and a computer code for the analysis of plates with closed branched and intersecting cracks are developed. The BEM enables simple and accurate modelling of cracked plates by using boundary elements. Contact tractions between crack surfaces are computed using an iterative procedure. Stress intensity factors (SIFs) are determined using the path-independent integral. Three numerical examples are studied: a star-shaped crack in a square plate, multiple interacting cracks in an infinite plate and randomly distributed and intersecting cracks in a square plate. The examples demonstrate the simplicity of numerical modelling, the accuracy of the method and the possible applications. The influences of load directions, distances between cracks and the contact of the crack surfaces on SIF are investigated. For the plate with randomly distributed cracks, the effective elastic properties are additionally computed by considering or neglecting contact of crack surfaces. The results show that the importance of the contact procedure depends on how the cracked material is loaded.
Fedeliński P., Analysis of closed branched and intersecting cracks by the boundary element method, Acta Mechanica, Volume 233, Issue 3, Page 1213-1230 (2022),
DOI: DOI10.1007/s00707-022-03158-x

This paper reports on a theoretical framework to analyse coupled wave propagation in magnetoelectroelastic solids of hexagonal symmetry. The constitutive equations contain the effective properties of micromechanics to model piezoelectric–piezomagnetic composites. The Mori–Tanaka scheme is used. The governing equations include the elastodynamic equations of motions and unique forms of the Maxwell equations for electromagnetics. The result is a set of fifteen first-order, fully coupled, hyperbolic partial differential equations with velocities, elastic stress components, and electromagnetic fields as the unknowns and as the components of the state vector. The structural analysis of the introduced equation set is performed, and the hyperbolicity is formally proved. The physics of coupled acoustic–electromagnetic wave propagation are fully described by the eigenstructure of matrices included in the considered system of equations. In particular, the eigenvalues of the main matrix pencil are the wave speeds, and a part of the left eigenvectors represents the coupled-wave polarization. The spectrum of the main matrix pencil shows the two-scale structure with the gap between mainly electromagnetic and mainly acoustic coupled modes. The analysis of the two-scale system dynamics is also performed. The small parameter is identified, and the slow–fast decomposition is obtained. The slow subsystem in the two-time-scale model is identified as the so-called quasi-static approximation of the magnetoelectroelastic continuum dynamics.

This study aims to develop a time‐efficient and accurate method for estimating the effective nonlinear behaviour of composites reinforced with misaligned short fibres. The ground‐breaking aspect of the proposed approach is combining the two‐stage hybrid homogenization method with the novel formulation of the pseudo‐grain discretization method. The numerical solution of the equivalent inclusion problem is conducted in the first homogenization stage for the finite number of pseudo‐grains. The obtained solution can be generalized for arbitrary orientation distribution and volume fraction of fibres during the time‐efficient second homogenization stage. The proposed method's accuracy has been verified both in linear elastic and elastic– plastic regimes by comparing the obtained results with reference solutions achieved by using wellestablished analytical and numerical methods.

In the paper, the numerical analysis of heat and mass transfer proceeding in an axially symmetrical articular cartilage sample subjected to the cryopreservation process is presented. In particular, a two-dimensional (axially symmetrical) model with imprecisely defined parameters is considered. The base of the heat transfer model is given by the interval Fourier equation and supplemented by initial boundary conditions. The phenomenon of cryoprotectant transport (Me2SO) through the extracellular matrix is described by the interval mass transfer equation. The liquidustracking (LT) method is used to control the temperature, which avoids the formation of ice regardless of the cooling and warming rates. In the LT process, the temperature decreases/increases gradually during addition/removal of the cryoprotectant, and the articular cartilage remains on or above the liquidus line so that no ice forms, independent of the cooling/warming rate. The discussed problem is solved using the interval finite difference method with the rules of directed interval arithmetic. Examples of numerical computations are presented in the final part of the paper. The obtained results of the numerical simulation are compared with the experimental results, realized for deterministically defined parameters.
The paper reports the new forms of the fundamental solutions for 3D magnetoelectroe- elasticity equations. The state-of-art presented in the paper shows that the fundamental solutions for magnetoelectroelasticity equations take complex forms, especially considering their applications in the boundary element method. In the paper, the magneto-electroelastic continuum serves as a homogenized model of the piezoelectric-piezomagnetic composites. The model is obtained by the Mori-Tanaka micromechanical approach. The so-called quasi-static approximation of dynamics is applied to obtain the set of the partial differential equations consists of the hyperbolic equation of motion and two elliptic equations for the conservation laws of the electric and magnetic charge. The motivation example shows the analogy between the impulse response of the linear system of ordinary differential equations, known from the classical linear control theory, and the fundamental solution of the linear system of partial differential equations. The spatial Fourier transform changes the coupled system of hyperbolic-elliptic equations of magneto-electro-elasticity into differential-algebraic equations in the k-space and the time domain. Instead of the classic approach eliminating the constraint equations for the electromagnetic static potentials, the semi-state vector is introduced and the descriptor system with the Kronecker index equals 1 is obtained. The structural analysis is performed for the resultant system and the regular and singular matrix pencils were analyzed. The slowness surfaces of the mainly acoustic modes in the quasi-static approximation are constructed for the 3- phase composite. Further, the shifting method is applied and the general solution of the semi-state equations is obtained as an analogon of the impulse response solution. The obtained result serves as a base for obtaining the new form of the fundamental solution of dynamic magnetoelectroelasticity in 3-dimensional space and also for the step response and steady-state fundamental solution for magnetoelectroelastic continuum.

A single blood vessel surrounded by the biological tissue with a tumor is considered. The influence of the heating technique (e.g. ultrasound, microwave, etc.) is described by setting a fixed temperature for the tumor which is higher than the blood and tissue temperature. The temperature distribution for the blood sub-domain is described by the energy equation written in the dual-phase lag convention, the temperature distribution in the biological tissue with a tumor is described also by the dual-phase lag equation. The boundary condition on the contact surface between blood vessel and biological tissue and the Neumann condition are also formulated using the extended Fourier law. So far in the literature, the temperature distribution in a blood vessel has been described by the classical energy equation. It is not clear whether the Fourier's law applies to highly heated tissues in which a significant thermal blood vessel is distinguished, therefore, taking into account the heterogeneous inner structure of the blood, the dual-phase lag equation is proposed for this sub-domain. The problem is solved by means of the implicit scheme of the finite difference method. The computations were performed for various values of delay times, which were taken from the available literature, and the influence of these values on the obtained temperature distributions was discussed.

The kinetics of heat transfer in hardening concrete is a key issue in engineering practice for erecting massive concrete structures. Prediction of the temperature fields in early age concrete should allow for proper control of the construction process to minimize temperature gradients and the peak temperatures, which is of particular importance for concrete durability. The paper presents a method of identification of the thermophysical parameters of early age concrete such as the thermal conductivity, the specific heat, and the heat generated by cement hydration in time. Proper numerical models of transient heat conduction problems were formulated by means of finite-element method, including two types of heat losses. The developed experimental–numerical approach included the transient temperature measurements in an isolated tube device and an inhouse implementation of an evolutionary algorithm to solve the parameter identification task. Parametric Bezier curves were proposed to model heat source function, which allowed for identifying such function as a smooth curve utilizing a small number of parameters. Numerical identification tasks were solved for experimental data acquired on hardening concrete mixes differing in the type of cement and type of mineral aggregate, demonstrating the effectiveness of the proposed method (the mean-squared error less than 1 °C). The proposed approach allows for the identification of thermophysical parameters of early age concrete even for mixtures containing non-standard components while omitting drawbacks typical for classical optimization methods.

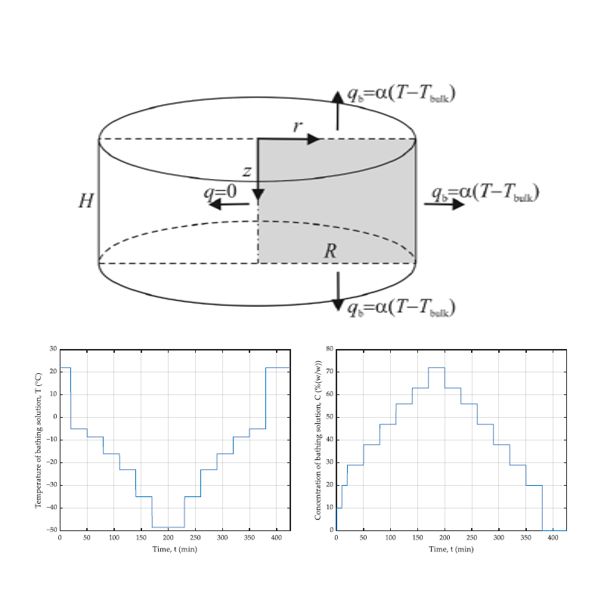
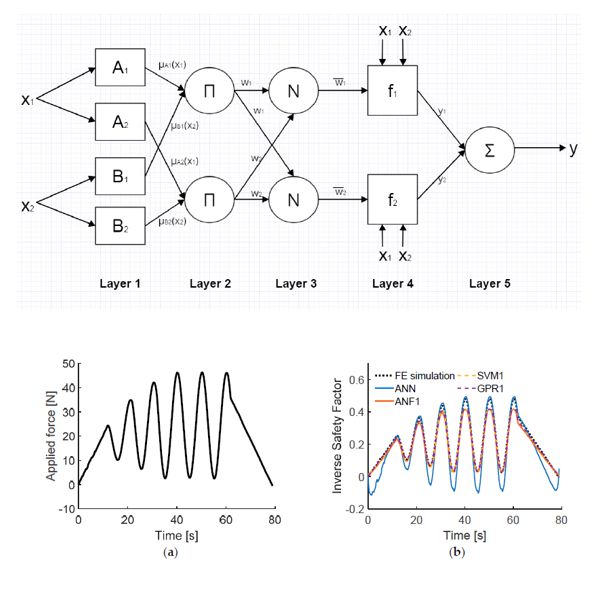
Operational Load Monitoring consists of the real-time reading and recording of the number and level of strains and stresses during load cycles withstood by a structure in its normal operating environment, in order to make more reliable predictions about its remaining lifetime in service. This is particularly important in aeronautical and aerospace industries, where it is very relevant to extend the components useful life without compromising flight safety. Sensors, like strain gauges, should be mounted on points of the structure where highest strains or stresses are expected. However, if the structure in its normal operating environment is subjected to variable exciting forces acting in different points over time, the number of places where data will have be acquired largely increases. The main idea presented in this paper is that instead of mounting a high number of sensors, an artificial neural network can be trained on the base of finite element simulations in order to estimate the state of the structure in its most stressed points based on data acquired just by a few sensors. The model should also be validated using experimental data to confirm proper predictions of the artificial neural network. An example with an omega-stiffened composite structural panel (a typical part used in aerospace applications) is provided. Artificial neural network was trained using a high-accuracy finite element model of the structure to process data from six strain gauges and return information about the state of the panel during different load cases. The trained neural network was tested in an experimental stand and the measurements confirmed the usefulness of presented approach.
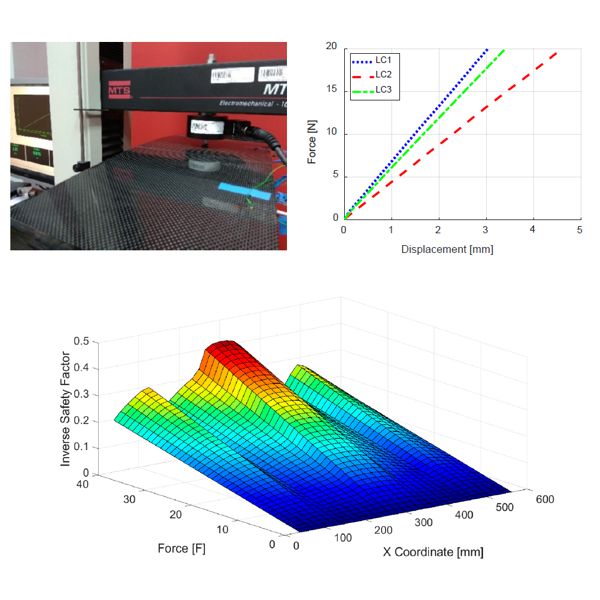
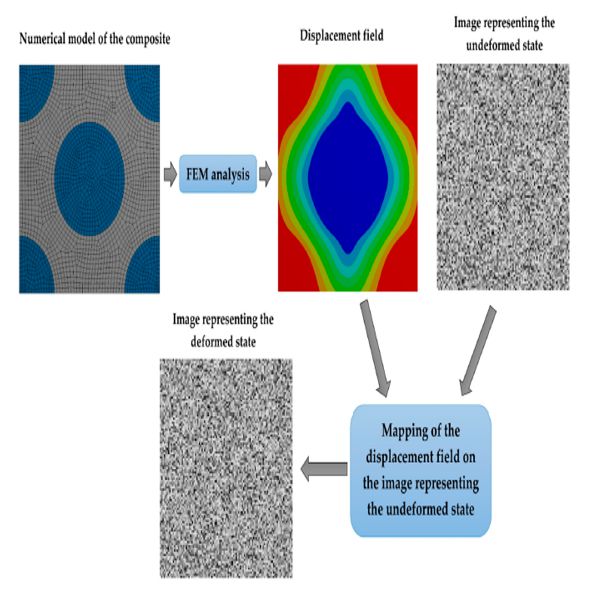
This paper is devoted to numerical and experimental investigation of the strain field at the level of the constituents of two-phase particle reinforced composite. The research aims to compare the strain distributions obtained experimentally with the results obtained by using a computational model based on the concept of the representative volume element. A digital image correlation method has been used for experimental determination of full-field strain. The numerical investigation was conducted by the finite element analysis of the representative volume element. Moreover, usage of the novel method of assessment of the speckle pattern applicability for the measurement of local fields by using the digital image correlation method has been proposed. In general, the obtained experimental and numerical results are in good agreement although some discrepancies between the results have been noticed and discussed.
The aim of this study was to elaborate on the methods of constructing combined components of a car mirror. The components were made of materials with different thermal expansion coefficient. The basis for the research were numerical simulations prepared in Moldex 3D software. The external cover of a mirror would be made of carbon composite based on epoxy resin (hereafter referred to as carbon), and the internal insert would be made of ABS. The adhesive bonding applied did not provide appropriate properties and led to breaks during usage. After carrying out moldflows it was found that the areas of breaks were determined by the places where fronts of flowing material met during the injection. The cause of breaking was diametrically different thermal expansion of both materials. This induced significant stresses in the adhesive layer. Finally, the effective solution was to change the geometry of the mirror insert made of thermoplastic ABS

The aim of operational load monitoring is to make predictions about the remaining usability time of structures, which is extremely useful in aerospace industry where in-service life of aircraft structural components can be maximized, taking into account safety. In order to make such predictions, strain sensors are mounted to the structure, from which data are acquired during operational time. This allows to determine how many load cycles has the structure withstood so far. Continuous monitoring of the strain distribution of the whole structure can be complicated due to vicissitude nature of the loads. Sensors should be mounted in places where stress and strain accumulations occur, and due to experiencing variable loads, the number of required sensors may be high. In this work, different machine learning and artificial intelligence algorithms are implemented to predict the current safety factor of the structure in its most stressed point, based on relatively low number of strain measurements. Adaptive neuro-fuzzy inference systems (ANFIS), support-vector machines (SVM) and Gaussian processes for machine learning (GPML) are trained with simulation data, and their effectiveness is measured using data obtained from experiments. The proposed methods are compared to the earlier work where artificial neural networks (ANN) were proven to be efficiently used for reduction of the number of sensors in operational load monitoring processes. A numerical comparison of accuracy and computational time (taking into account possible real-time applications) between all considered methods is provided.
The aim of the work is to analyse the effective elastic properties of composites with randomly distributed thin rigid fibres. The matrix is linear-elastic, homogenous and isotropic, and the fibres are perfectly connected to the matrix. Two-dimensional models of composites are analysed using the boundary element method (BEM). The method requires division of fibres and external boundaries of the plate into boundary elements. The boundary quantities are interpolated using quadratic shape functions. The direct solutions are: displacements and tractions along the external boundaries, displacements of fibres and interaction forces between the fibres and the matrix. Three numerical examples are presented in the paper: a single fibre in a circular disc, uniformly distributed parallel fibres and randomly distributed and oriented fibres in a square plate. The influence of distribution and orientation of fibres on effective Young’s moduli, Poisson’s ratios and Kirchhoff’s moduli is analysed. The examples demonstrate the accuracy and efficiency of the method.
Fedeliński P., Effective elastic properties of composites with randomly distributed thin rigid fibres, Archive of Applied Mechanics, Volume 91, Issue 1, Page 135-149 (2020),
DOI10.1007/s00419-020-01758-4

The present paper is devoted to the theoretical study on the estimation of the full-field strain at the microstructural level of composite materials by means of Digital Image Correlation (DIC). The main aim of the paper is to investigate the influence of speckle size on the accuracy of the strain field measurement at the microscale. The DIC analysis was conducted based on artificial speckle patterns generated numerically and the deformation behavior of the composites was simulated by using the finite element method (FEM). This approach gives the opportunity to compare the results of the DIC in terms of speckle size with the reference FEM solution. Moreover, the paper focuses on the inverse identification of the material constants of the composite constituents by using information associated with the measured strain field. The inverse problem is solved by using a novel two-step optimization procedure, which reduces the problem complexity. The feasibility and accuracy of the proposed approach are presented by analysis of two exemplary microgeometries representing the microstructures of fiber reinforced composites.
In oncology, hyperthermia is understood as a planned, controlled technique of heating cancerous changes in order to destroy their cells or stop their growth. In clinical practice, hyperthermia is used in combination with radiotherapy, chemotherapy, or immunological therapy. During the hyperthermia, the tissue is typically exposed to a temperature in the range of 40–45 _C, the exception is thermoablation, during which the temperatures reach much higher values. Thermoablation is characterized by the use of high temperatures up to 90 _C. The electrode using the radiofrequency is inserted into the central area of the tumor. Interstitial thermoablation is used to treat, among others, breast and brain cancer. The therapy consists of inducing coagulation necrosis in an area that is heated to very high temperatures. Mathematical modeling is based on the use of a coupled thermo-electric model, in which the electric field is described by means of the Laplace equation, while the temperature field is based on the Pennes equation. Coupling occurs at the level of the additional source function in the Pennes equation. The temperature field obtained in this way makes it possible to calculate the Arrhenius integral as a determinant of the destruction of biological tissue. As a result of numerical calculations regarding the temperature field and the Arrhenius integral, it can be concluded that, with the help of numerical tools and mathematical modeling, one can simulate the process of destroying cancerous tissue.

The paper presents the application of the IMGAMO (immune game theory multiobective algorithm) in the optimal design of electrothermal microactuators. Several numerical tests on the mathematical benchmark test functions were performed, showing the superiority of the IMGAMO, when a large number of criteria are considered, in comparison to other multiobjective optimizers. A parametric numerical model of an electrothermal microactuaror was developed and verified. Six functionals, which depend on various thermal and mechanical quantities of the microactuator, were proposed, formulated and numerically implemented. These functionals represent real requirements asked of microactuators. The boundary-value problem of an electro-thermo-mechanical field was solved multiple times during the course of optimization by way of the finite element method (FEM). A numerical example of multiobjective optimization of chevron-type electrothermal actuators is included in the paper. Representation of the multi-dimensional Pareto fronts by means of scatter plot matrices, aided by self-organizing maps (SOMs), is presented. The novel method of selecting interesting, compromise-solutions is proposed and described.
Thermal processes in domain of thin metal film subjected to an ultrashort laser pulse are considered. A mathematical description of the process discussed is based on the system of four equations. Two of them describe the electrons and lattice temperature, while third and fourth equations represent the generalized Fourier law, it means the dependencies between the electrons (lattice) heat flux and the electrons (lattice) temperature gradient. In the generalized Fourier law the heat fluxes are delayed in relation to the temperature gradients which consequently causes the appearance of heat fluxes time derivatives in the appropriate equations. Depending on the order of the generalized Fourier law expansion into the Taylor series, the first- and the second-order model can be obtained. In contrast to the commonly used first-order model, here the second-order two-temperature model is proposed. The problem is solved using the implicit scheme of the finite difference method. The examples of computations are also presented. It turns out that for the low laser intensities the results obtained using the first- and the second-order models are very similar.

Heat transfer processes occurring in 3D bi-layered microdomain subjected to the ultra-short laser pulse are con- sidered. The problem is described by the system of two dual-phase lag equations supplemented by appropriate boundary and initial conditions. The ideal contact condition at the interface between the layers in the case of the dual-phase lag model is formulated in a different way than in the macroscopic Fourier one. To solve the problem the general boundary element method is proposed. In the final part of the paper the examples of computations are presented, and the conclusions are formulated.

© Silesian University of Technology
The authors - the organizational units in which the information materials were produced, are fully responsible for the correctness, up-to-date and legal compliance with the provisions of the law. Hosted by: IT Center of the Silesian University of Technology (www@polsl.pl)
„E-Politechnika Śląska - utworzenie platformy elektronicznych usług publicznych Politechniki Śląskiej”